Motion

This is a section that talks about forces and motion, discussing and covering all the important topics that you need to know for your IGCSE Physics examinations.
A force has the potential to cause a body to:
• Accelerate
• Decelerate
• Change direction
• Change shape
Important forces

There are some important forces that you need to know:
1. Weight: the weight of an object is the pull of gravity on it. Weight always acts vertically downwards.
2. Friction: is a force which opposes motion. Friction always acts in the opposite direction of any force.
3. Air resistance: is the force of friction when an object moves through air or water.
4. Upthrust: is the upward push of a liquid or a gas on an object.
Energy Skate Park Simulator
Through the Energy scate park simulator, you will gain a better and stronger understanding of Motion for IGCSE Physics. Toggle between the playground to see how different types of forces have different effects on the skater. This is a fun way to understand Motion and forces acting on the skater. You can also view the simulator as a graph to show the graphical representation of kinetic and potential forces acting on the skater during different stages of motion.
Force = mass x acceleration
F = ma
Speed and Velocity
Speed is the distance travelled per unit time.
In simple words, speed is the distance you travel in a specific amount of time.
The units used for Speed are the following:
m/s (metres per second)
km/h (kilometer per hour)
Please note that speed is a scalar quantity and does not have a direction.
Velocity is almost the same as speed, except for one major difference: velocity has a direction and, therefore, is a vector quantity.
In other words, velocity is the distance you travel in a specific amount of time in a specific direction.
To calculate velocity, we use the following formula:
v = s / t
Velocity = total distance traveled / total time taken
Acceleration
Acceleration is the change in velocity per unit time. In simpler words, acceleration is the increase or decrease of velocity in a given time.
To calculate acceleration, we use the following formula:
a = Δv/Δt
The symbol Δ (read as 'delta' after the Greek alphabet) means change. So Δ means a change in velocity (final - initial) or (v-u).
In the formula above, a is the acceleration
Δv is a change in velocity
Δt is the change in time, in simple words, how long it took.
Speed-time graphs
A speed-time graph shows how an object’s speed changes over time using a line or curve on a graph.
For example, in the table below, we have the speed of an object at intervals of 1 second.
| Time (s) | Speed (m/s) |
|---|---|
| 1 | 10 |
| 2 | 10 |
| 3 | 10 |
| 4 | 10 |
| 5 | 10 |
As you can see, the speed of the object does not change at all during the 5 seconds. We can say that this object has a constant speed. This means that the graph of the object will be a straight line.
A graph for the table has been drawn below:
Made with Visme
(feel free to hover around the graph- it is made to be interactive).
For an object which is accelerating as shown in the table below:
| Time (s) | Speed (m/s) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 9 |
| 5 | 12 |
The graph for this object would be like this:
Made with Visme
We can say that this object is accelerating at a constant acceleration since the graph is not a curve.
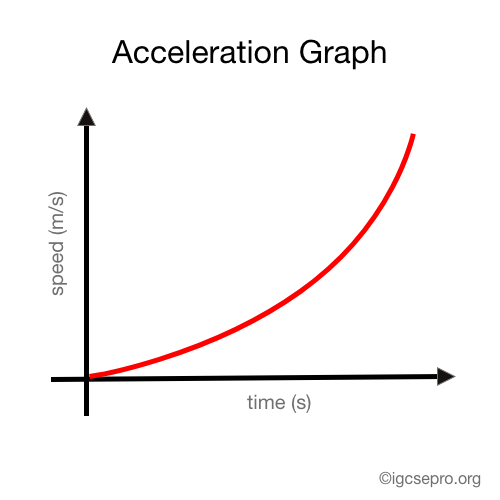
However, when the graph is a curve similar to the one below, we can say the acceleration is not constant, therefore changing acceleration.
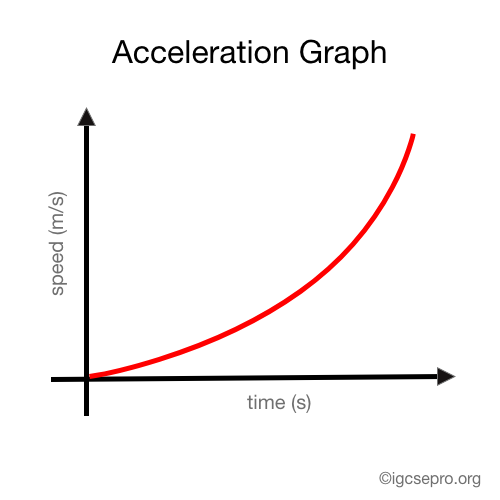
Calculating the acceleration in a speed-time graph
The method is similar to one given below to calculate speed from a distance-time graph.
Calculating distance from speed-time graph
To calculate distance from a speed-time graph, we calculate the area under it.
For example, in the graph below, you can see a graph of an object that is constantly accelerating first and then has a constant speed.
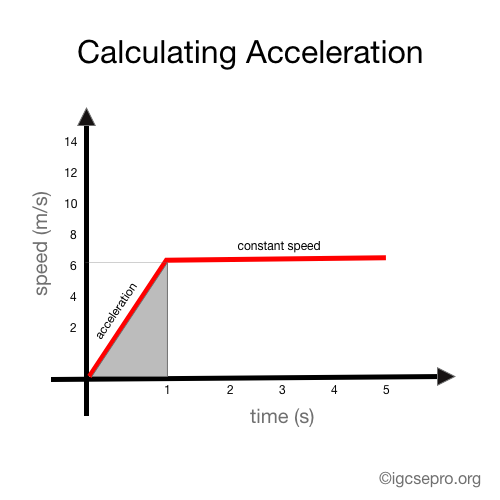
Now, we calculate the area of the triangle, which would be: 1 × 4 × (1/2) which equals to 2.
Next, we calculate the area of the rectangle.
time = 5 - 1 = 4 s
speed = 4 m/s
So the area would be 4 x 4, which is equal to 16.
Therefore, the total area would be which is 18. The distance traveled by the object would be 18 meters.
Distance-time graphs
A distance-time graph shows how the distance traveled by an object changes over time using a line or curve on a graph.
The distance-time graph of an object moving at a constant speed would be similar to the one below (a slanted straight line, not a curve):
Made with Visme
And the distance-time graph of an object at rest would be similar to this (a straight line):
Made with Visme
The distance-time graph of accelerating and decelerating objects would be similar to this:
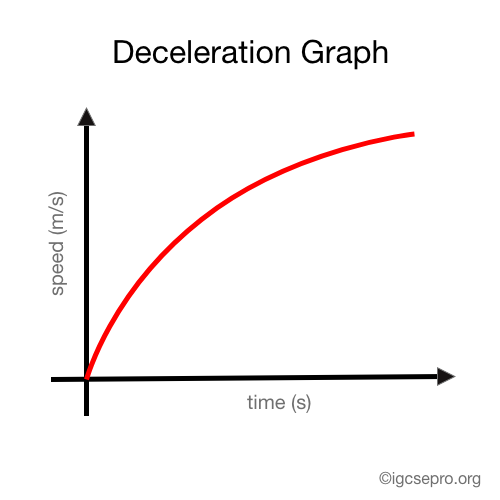
Note
Deceleration is negative acceleration.
If deceleration = 2 m/s^2, then acceleration will be -2 m/s^2
Calculating speed from a distance-time graph of an object at constant speed
To calculate the speed of an object at constant speed from its distance-time graph, we use the gradient of the line.
To calculate the gradient, we do the following:
Take any 2 points on the line, for example we can take (1, 2) and (2, 6).
Remember, we always write the x coordinate first. (x, y)
Use the following formula to calculate the gradient:
(y2-y1)/(x2-x1)
So, we will do:
(6 - 2)/(2 - 1)
Which will give us:
4/1 or 4.
Therefore, the speed of the object is 4 m/s.
The three equations of motion
An easier way to solve sums is using the three equations of motions.
But first you need to know what symbol represents what:
v = final velocity
u = initial velocity
a = acceleration
t = time
s = distance
g = gravity (acceleration of free fall) = 9.8 m/s2
unless the paper (information on first page of paper)/question specifically mentions to take another value.
1. First equation: v = u + at
2. Second equation: s = ut + (1/2)at^2
3. Third equation: v^2 - u^2 = 2as
Free fall

Free fall is when an object falls freely under the influence of gravity alone, without any other forces affecting its motion.
Air resistance is a force that slows down objects falling through the air. It is also known as drag.
The question will usually mention whether to ignore air resistance or not.
When an object is in free fall, it’s acceleration will be 9.8 m/s^2 (or 10 m/s^2, depending on the question).
Without air or liquid resistance, falling objects accelerate continuously. However, with resistance, their acceleration decreases and they eventually reach a constant speed known as terminal velocity.
Note
A heavier object and a lighter object when dropped from the same distance, will reach the ground at the exact same time.
The object's mass is not considered in a free fall (as long as air resistance is ignored).
The acceleration of a freely falling body does not depend on the mass of the body.
***this is the end of this guide. Hope you enjoyed it! Thanks for using Igcsepro.org! We hope you will give us a chance to serve you again! Thank you!

